In our daily life, the Cubic foot plays an important role. If we look up our daily routine, oftentimes we hear this word, if we are going to build a new house the blue-collar worker and the contractor usually say “Cubic foot or cubic feet” during their work. The term cubic feet is commonly used in the numerical problems of Physics and Mathematics.
In this article, we will study the basic definition of cubic feet its calculation and conversion with the help of different examples.
Definition:
Table of Contents
According to Wikipedia:
The Cubic foot (symbol ft3 or cu ft.) is an imperial and US customary (non-metric) unit of volume, used in the United States and the United Kingdom. It is defined as the volume of a cube with sides of one foot (0.3048 m) in length.
Formula:
Cubic feet = Length (feet) × Width (feet) × Height (feet)
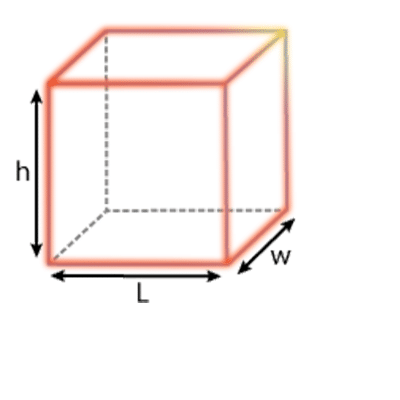
Calculation:
Calculation of the cubic feet is not too complex but it takes time. The multiplication process is used in calculating cubic feet.
There are two different cases of calculating volume in cubic feet:
1) If the values (Length width and height) are given in feet.
2) If the values (Length width and height) are given in any other unit.
Case-I: If the values (Length width and height) are given in feet.
If the values/given data is in feet then the calculation is quite simple.
Example#1:
Calculate the volume (in cubic feet) of a cube of height 6 ft., Length 5 ft., and width 4 ft.
Solution:
Step-I: Extract the given data from the problem
Length= 5 ft.
Width= 4 ft.
Height= 6 ft.
Formula:
Volume (Cubic feet) = Length (feet) × Width (feet) × Height (feet)
Step-II: Put the values in the formula
Volume = Length (feet) × Width (feet) × Height (feet)
Volume = 5ft × 4ft × 6ft
Volume = 120 ft3 which is our required answer
Example#2:
Calculate the volume (in cubic feet) of a beaker of height 0.5 ft., Length 0.3 ft., and width 0.335 ft.
Solution:
Given data:
Length= 0.3 ft.
Width= 0.335 ft.
Height= 0.5 ft.
Formula:
Volume (Cubic feet) = Length (feet) × Width (feet) × Height (feet)
Calculations:
Volume = Length (feet) × Width (feet) × Height (feet)
Volume = 0.3ft × 0.335ft × 0.5ft
Volume = 0.05 ft3 which is our required answer.
Case-II: If the values (Length width and height) are given in any other unit.
In this case, we will study the conversion of different units. Normally, in different numerical problems values are given in feet but if you got values (length, width, and height) in any other units then you don’t need to worry about that, you just have to follow some extra steps of conversion.
Subcase-I: If the values are given in meters
Example:
Calculate the volume (in cubic feet) of a cube of height 0.3 meters, Length 0.25 meters, and width 0.7 meters.
Solution:
Step-I: Extract the given data from the problem
Given data:
Length= 0.3 meters
Width= 0.25 meters
Height= 0.7 meters
Formula:
Volume (Cubic feet) = Length (feet) × Width (feet) × Height (feet)
Step-II: Conversion (convert the given data into feet)
Before putting these values in the formula, we have to convert the values first.
As we know “1 meter” is equal to “3.2808 feet”
We will multiply all values by “3.2808” to convert them into feet
Length= 0.3 × 3.2808= 0.943 ft.
Width= 0.25 × 3.2808=0.82025 ft.
Height= 0.7 × 3.2808=2.2967 ft.
Step-III: Put the values in the formula
Calculations:
Volume = Length (feet) × Width (feet) × Height (feet)
Volume = 0.984 ft. × 0.82 ft. × 2.297 ft.
Volume = 1.85 ft3 which is our required answer
Subcase-II: If the values are given in yards
Example:
Calculate the volume (in cubic feet) of a cage of height 1.8 yards, Length 2 yards, and width 0.9 yards.
Solution:
Given data:
Length= 2 yards
Width= 0.9 yards
Height= 1.8 yards
Formula:
Volume (Cubic feet) = Length (feet) × Width (feet) × Height (feet)
Before putting these values in the formula, we have to convert the values first.
As we know “1 yard” is equal to “3 feet”
We will multiply all values by “3” to convert them into feet
Conversion:
Length= 2×3 = 6 ft.
Width= 0.9 × 3 = 2.7 ft.
Height= 1.8 × 3 = 5.4 ft.
Calculations:
Volume = Length (feet) × Width (feet) × Height (feet)
Volume = 6 ft. × 2.7 ft. × 5.4 ft.
Volume = 87.48 ft3 which is our required answer
To get rid of these long calculations you can also use a Cubic feet calculator to solve numerical problems with one click.
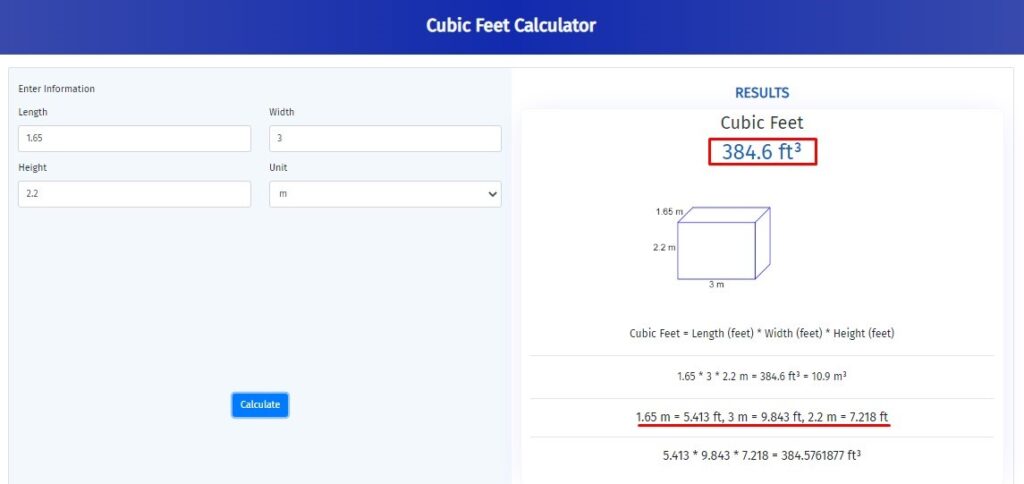
This online cubic feet calculator is very useful and user friendly you can easily calculate the volume in
Cubic Feet using this free online Cubic feet calculator.
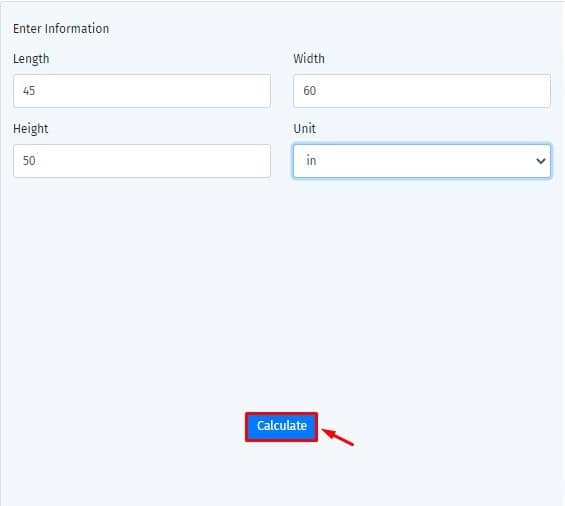
How to use the cubic feet calculator?
You just have to follow these simple steps:
1) Enter the length, width, and height in the given input boxes.
2) Select the unit of the measurement from the dropdown menu.
3) Click on the Calculate button to see the result.
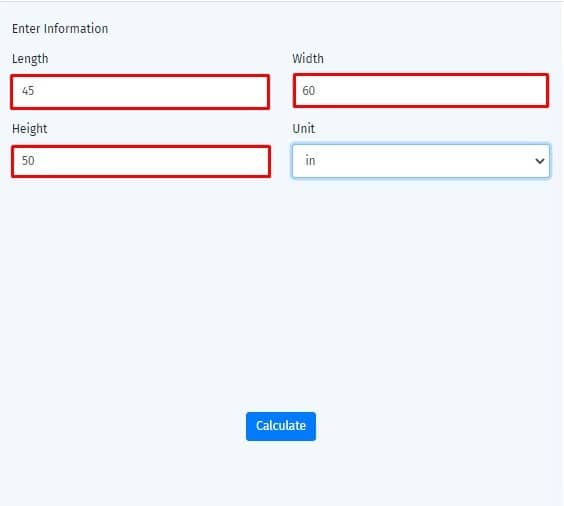
STEP-I
Enter length, width, and height in the given input boxes.
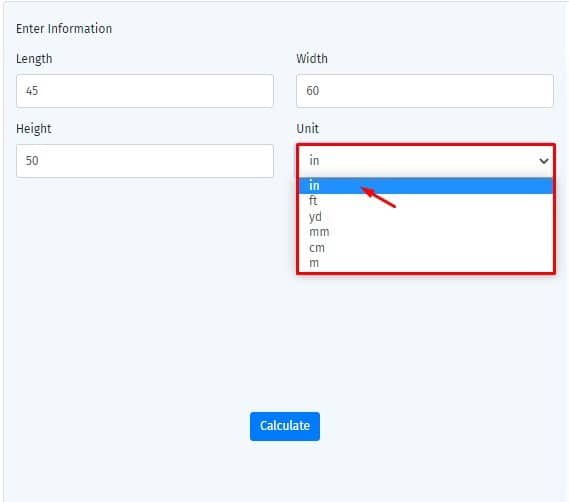
STEP-II
Select the unit of the measurement from the dropdown menu.
STEP-III
Click on the Calculate button to see the result.
You will get the answer in cubic feet, the calculator automatically converts the given input units into Cubic feet and meters (meter SI unit of length).
Conversion:
In the above section, we have read about converting the unit “meter” to “feet”. Now the following table will help you in converting the given quantities into feet after that your calculations will become easier.
Some commonly used units are given in the following table.
| Units | Value in feet | Cubic values | Conversion in ft3 |
| 1 meter | 3.28084 | 1 cubic meter | 35.3147 |
| 1 cm | 0.0328084 | 1 cubic cm | 3.53147e-5 |
| 1 in | 0.0833333 | 1 cubic inch | 0.000578 |
| 1 yd. | 3 | 1 cubic yard | 27.00 |
| 1 mm | 0.00328084 | 1 cubic mm | 3.5314666E-8 |
These are the units that are usually used in numerical problems and we commonly use them in our daily routine.
With this table, we can learn the values and remember them easily, instead of searching all the values separately on the search engine or in different books, use this table to make your calculations easier.
Summary:
In this article, we have studied the basic definition of a cubic foot, its conversion, and calculations.
Now, you have learned about all the basics of cubic feet. You can solve any problem related to cubic feet by following the examples and table of this article.

